How To Find The Solution Set Of A Logarithmic Equation

Solving Logarithmic Equations

Generally, there are two types of logarithmic equations. Study each example advisedly before you start looking at the worked examples below.

Types of Logarithmic Equations

• The kickoff blazon looks like this.

If you lot have a single logarithm on each side of the equation having the same base, you can prepare the arguments equal to each other and so solve. The arguments here are the algebraic expressions represented by \color{bluish}M and \color{scarlet}Due north.

• The second blazon looks like this.

If y'all take a single logarithm on one side of the equation, yous tin express information technology as an exponential equation and solve information technology.

Let's learn how to solve logarithmic equations past going over some examples.

---

Examples of How to Solve Logarithmic Equations

Example one: Solve the logarithmic equation.

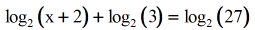
Since we desire to transform the left side into a single logarithmic equation, we should use the Production Rule in reverse to condense information technology. Here is the dominion, merely in case y'all forgot.

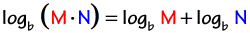
• Given

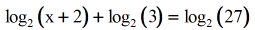
• Utilise Product Rule from Log Rules.

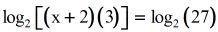
• Distribute: \left( {x + two} \right)\left( iii \right) = 3x + 6

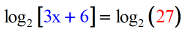
• Drib the logs, prepare the arguments (stuff inside the parenthesis) equal to each other.

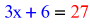
• Then solve the linear equation. I know you got this role downwardly!

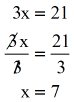
Merely a big caution. Ever check your solved values with the original logarithmic equation.

Remember:

• It is OKAY to accept values of x such as positive, 0, and negative numbers.
• Withal, information technology is Not ALLOWED to have a logarithm of a negative number or a logarithm of aught, 0, when substituted or evaluated into the original logarithm equation.

Circumspection: The logarithm of a negative number, and the logarithm of nil are both not defined.

{\log _b}\left( {{\rm{negative\,\,number}}} \right) = {\rm{undefined}}

{\log _b}\left( 0 \right) = {\rm{undefined}}

Now, permit'southward cheque our answer if 10 = 7 is a valid solution. Substitute dorsum into the original logarithmic equation and verify if it yields a truthful statement.

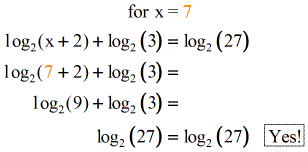
Yes! Since x = 7 checks, we have a solution at \colour{blue}10 = vii.

---

Case ii: Solve the logarithmic equation.

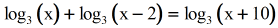
Starting time past condensing the log expressions on the left into a single logarithm using the Product Rule. We want to take a unmarried log expression on each side of the equation. Be prepare, though to solve for a quadratic equation since x will have a power of two.

• Given

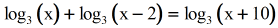
• Utilise Product Rule from Log Rules

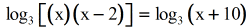
• Simplify: \left( x \right)\left( {x - 2} \right) = {ten^2} - 2x

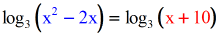
• Driblet the logs, set the arguments (stuff inside the parenthesis) equal to each other

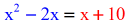
• Solve the quadratic equation using the factoring method. But you need to move everything on one side while forcing the opposite side equal to 0.

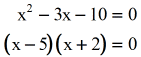
• Set up each gene equal to zero, then solve for x.

x - 5 = 0 implies that x = v

x + 2 = 0 implies that x = - ii

So the possible solutions arex = five and10 = - 2.  Remember to ever substitute the possible solutions dorsum to the original log equation.

Let's bank check our potential answers x = 5 and 10 = - 2 if they will be valid solutions. Substitute back into the original logarithmic equation and verify if it yields a truthful statement.

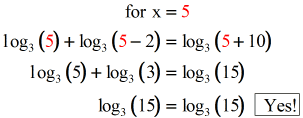
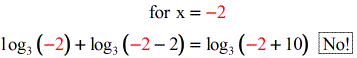
After checking our values of x, we found that x = 5 is definitely a solution. However, x =-ii generates some negative numbers inside the parenthesis ( log of zero and negative numbers are undefined) that makes united states eliminate x =-2 as function of our solution.

Therefore, the final solution is only \color{bluish}x=five. We disregard x=-ii because it is an extraneous solution.

---

Example iii: Solve the logarithmic equation.

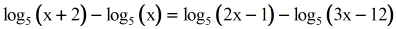
This is an interesting problem. What we have here are differences of logarithmic expressions on both sides of the equation. Simplify or condense the logs on both sides past using the Quotient Rule, which looks like this.

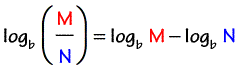
• Given

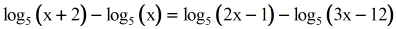
• The difference of logs is telling us to use the Quotient Rule. Convert the subtraction operation exterior into a division functioning inside the parenthesis. Practise it to both sides of the equations.

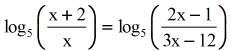
• I think we are ready to set up each argument equal to each other since we can reduce the problem to have a single log expression on each side of the equation.

• Drop the logs, and set the arguments (stuff inside the parenthesis) equal to each other. Annotation that this is a Rational Equation. One way to solve it is to get its Cross Product.

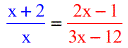
• Information technology looks similar this after getting its Cross Product.

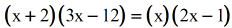
• Simplify both sides by the Distributive Property. At this point, we realize that it is merely a Quadratic Equation. No big deal and so. Movement everything to i side, which forces one side of the equation to be equal to cipher.

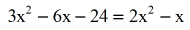
• This is easily factorable. At present set each factor to zero and solve for ten.

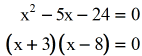
• So, these are our possible answers.

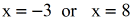
I will leave information technology to you to check our potential answers back into the original log equation. Yous should verify that \color{blue}x=8 is the only solution, while x =-3 is non since it generates a scenario wherein we are trying to become the logarithm of a negative number. Non practiced!

---

Example iv: Solve the logarithmic equation.

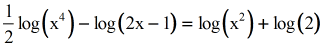
If you lot run across "log" without an explicit or written base, it is assumed to have a base of 10. In fact, a logarithm with base 10 is known every bit the common logarithm.

What we need is to condense or compress both sides of the equation into a single log expression. On the left side, we encounter a difference of logs which ways we utilise the Quotient Dominion while the right side requires the Product Dominion because they're the sum of logs.

There'south but one matter that you have to pay attention to on the left side. Do you run into that coefficient \Large{1 \over 2}\,?

Well, we have to bring it upwardly equally an exponent using the Ability Rule in reverse.

• Given

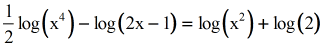
• Bring up that coefficient \large{1 \over 2} as an exponent (refer to the leftmost term)

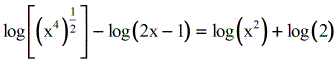
• Simplify the exponent (all the same referring to the leftmost term)

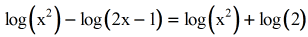
• And so, condense the logs on both sides of the equation. Use the Caliber Rule on the left and Product Rule on the correct.

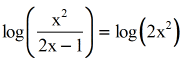
• Here, I used different colors to show that since we have the same base (if non explicitly shown it is assumed to be base x), it's okay to set them equal to each other.

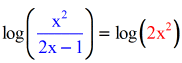
• Dropping the logs and only equating the arguments inside the parenthesis.

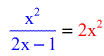
• At this point, you may solve the Rational Equation by performing Cross Product. Move all the terms on one side of the equation, and then factor them out.

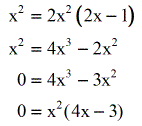
• Set each factor equal to zero and solve for x.

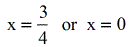
It's time to check your potential answers. When you cheque 10=0 back into the original logarithmic equation, you'll stop up having an expression that involves getting the logarithm of zippo, which is undefined, meaning – not expert! Then, we should disregard or drop \color{red}x=0 as a solution.

Checking \Big{ten = {iii \over four}}, confirms that indeed \Big{\color{blue}{x = {3 \over 4}}} is the simply solution.

---

Example 5: Solve the logarithmic equation.

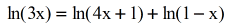
This problem involves the utilize of the symbol \ln instead of \log to mean logarithm.

Think of \ln as a special kind of logarithm using base of operations e where eastward \approx two.71828.

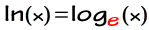
• Given

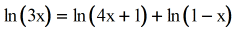
• Use Product Rule on the right side

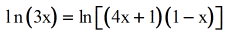
• Write the variable commencement, then the constant to be ready for the FOIL method.

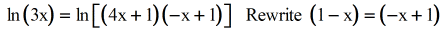
• Simplify the 2 binomials by multiplying them together.

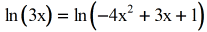
• At this point, I simply color-coded the expression within the parenthesis to imply that we are fix to set them equal to each other.

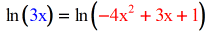
• Aye! This is where nosotros say that the stuff inside the left parenthesis equals the stuff inside the correct parenthesis.

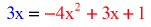
• Solve the Quadratic Equation using the Square Root Method. Y'all do it by isolating the squared variable on ane side and the constant on the other. Then we use the square root on both sides.

Don't forget the \pm symbol.

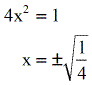
• Simplifying farther, nosotros should get these possible answers.

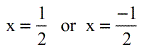
Check if the potential answers found above are possible answers by substituting them back to the original logarithmic equations.

Y'all should be convinced that the ONLY valid solution is \large{\color{blue}x = {one \over 2}} which makes \large{\color{red}x = -{1 \over ii}} an extraneous answer.

---

Example vi: Solve the logarithmic equation.

At that place is just i logarithmic expression in this equation. We consider this as the 2nd case wherein nosotros take

We will transform the equation from the logarithmic form to the exponential form, then solve it.

• Given

• I colour-coded the parts of the logarithmic equation to show where they go when converted into exponential form.

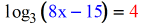
• The blueish expression stays at its current location, but the red number becomes the exponent of the base of operations of the logarithm which is iii.

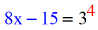
• Simplify the right side, {three^four} = 81.

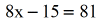
• Finish off by solving the two-pace linear equation that arises.

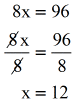
You should verify that the value \color{blue}10=12 is indeed the solution to the logarithmic equation.

---

Example 7: Solve the logarithmic equation.

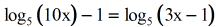
Collect all the logarithmic expressions on ane side of the equation (keep it on the left) and movement the constant to the right side. Employ the Quotient Rule to express the difference of logs as fractions inside the parenthesis of the logarithm.

• Given

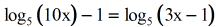
• Move all the logarithmic expressions to the left of the equation, and the constant to the right.

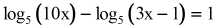
• Use the Quotient Rule to condense the log expressions on the left side.

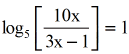
• Become ready to write the logarithmic equation into its exponential form.

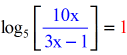
• The blue expression stays in its current location, just the red constant turns out to be the exponent of the base of operations of the log.

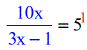
• Simplify the right side of the equation since five^{\color{red}1}=5.

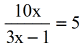
• This is a Rational Equation due to the presence of variables in the numerator and denominator.

I would solve this equation using the Cantankerous Product Rule. Simply I have to express starting time the right side of the equation with the explicit denominator of ane. That is, 5 = {\large{{5 \over 1}}}

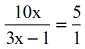
• Perform the Cross-Multiplication and then solve the resulting linear equation.

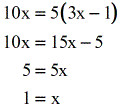
When yous check ten=1 back to the original equation, you should concord that \large{\color{blue}ten=i} is the solution to the log equation.

---

Example viii: Solve the logarithmic equation.

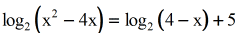
This problem is very similar to #7. Let's gather all the logarithmic expressions to the left while keeping the abiding on the right side. Since we accept the difference of logs, we will utilize the Caliber Dominion.

• Given

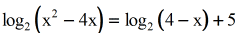
• Move the log expressions to the left side, and keep the constant to the correct.

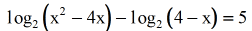
• Apply the Caliber Dominion since they are the difference of logs.

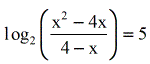
• I used different colors here to evidence where they become after rewriting in exponential course.

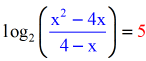
• Notice that the expression within the parenthesis stays in its current location, while the \color{cerise}5 becomes the exponent of the base.

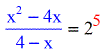
• To solve this Rational Equation, use the Cross Production Rule.

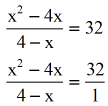
• Simplify the right side by the distributive belongings. It looks like we are dealing with a quadratic equation.

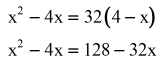
• Move everything to the left side and make the right side just zip.

Factor out the trinomial. Set up each factor equal to naught and then solve for x.

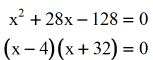
• When you solve for x, you should get these values of x every bit potential solutions.

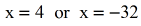
Make sure that you bank check the potential answers from the original logarithmic equation.

You should hold that \colour{blue}ten=-32 is the only solution. That makes \color{red}x=four an extraneous solution, then disregard information technology.

---

Example 9: Solve the logarithmic equation

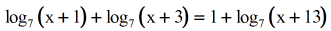
I promise yous're getting the principal idea now on how to approach this type of problem. Here we run across 3 log expressions and a constant. Permit's carve up the log expressions and the constant on contrary sides of the equation.

• Let's keep the log expressions on the left side while the abiding on the right side.

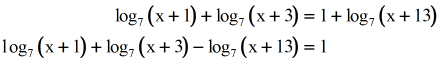
• Beginning by condensing the log expressions using the Product Rule to deal with the sum of logs.

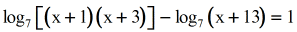
• Then further condense the log expressions using the Caliber Rule to deal with the difference of logs.

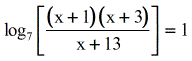
• At this betoken, I used different colors to illustrate that I'one thousand fix to limited the log equation into its exponential equation form.

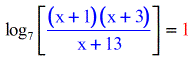
• Go along the expression within the grouping symbol ( blue ) in the same location while making the constant \color{ruby-red}1 on the correct side every bit the exponent of the base seven.

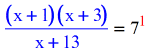
• Solve this Rational Equation using Cantankerous Production. Express 7 every bit \large{seven \over 1}.

• Cross multiply.

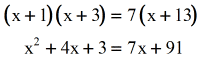
• Motility all terms to the left side of the equation. Factor out the trinomial. Next, set each gene equal to nada and solve for x.

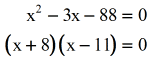
• These are your potential answers. Always check your values.

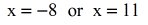
It's obvious that when we plug in x=-8 dorsum into the original equation, it results in a logarithm with a negative number. Therefore, yous exclude \color{red}10=-8 every bit office of your solution.

Thus, the only solution is \color{blue}x=11.

---

Example 10: Solve the logarithmic equation.

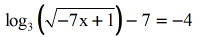
• Keep the log expression on the left, and motility all the constants on the right side.

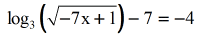
• Simplify.

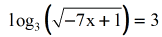
• I think nosotros're set to transform this log equation into the exponential equation.

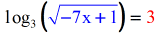
• The expression inside the parenthesis stays in its current location while the constant 3 becomes the exponent of the log base iii.

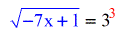
• Simplify the right side since {3^three}=27. What we accept here is a simple Radical Equation.

Bank check this split lesson if you demand a refresher on how to solve different types of Radical Equations.

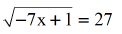
• To get rid of the radical symbol on the left side, square both sides of the equation.

• After squaring both sides, it looks like nosotros have a linear equation. But solve information technology as usual.

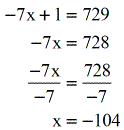
Check your potential respond back into the original equation.

After doing so, you should exist convinced that indeed \color{blue}10=-104 is a valid solution.

---

You might too exist interested in:

Condensing Logarithms

Expanding Logarithms

Logarithm Explained

Logarithm Rules

Source: https://www.chilimath.com/lessons/advanced-algebra/solving-logarithmic-equations/

Share this post